2024新奥正版资料免费提供,主成分分析法_UAG97.890精选版

　　在数据科学和统计分析领域，主成分分析法（PCA）是一种常用且强大的降维技术。它通过将原始数据转换为少数几个主要成分，帮助我们识别及解释数据中的重要特征。伴随着2024新奥正版资料的发布，我们将详细探讨主成分分析法及其在实际应用中的重要性与优越性，特别是针对UAG97.890版本的精选数据进行深入分析。

1. 主成分分析法的基本概念

　　主成分分析法旨在通过线性变换，将数据集转换到新的坐标系中，使得新的坐标系中的第一个轴（主成分1）具有最大的方差，第二个轴（主成分2）则在保证正交的基础上具有次大的方差，以此类推。通过这种方式，我们能够提取出数据中最重要的信息，降低数据维度，提高后续分析的效率。

1.1 PCA的使用步骤

　　主成分分析法的实施通常包括以下几个步骤：

1. 标准化数据：确保不同特征的量纲一致，避免某一特征对结果的过度影响。
2. 计算协方差矩阵：识别特征之间的关系，协方差矩阵能够反映数据各个维度之间的相互关联。
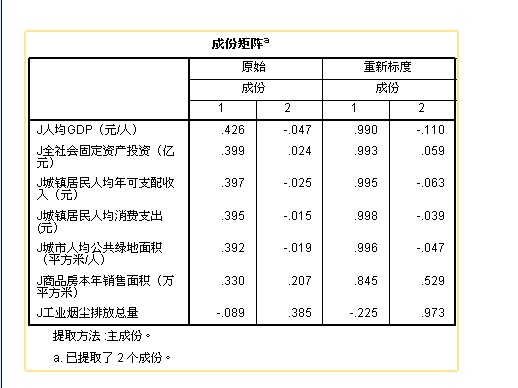
3. 特征值分解：从协方差矩阵中提取特征值和特征向量，以确定主成分的方向。
4. 选择主成分：根据特征值的大小选择前几个主成分，这些主成分将用于原始数据的降维。
5. 重新构造数据：将原始数据投影到选择的主成分上，从而实现降维。

1.2 数据可视化

　　通过主成分分析法，我们能够轻松实现数据的可视化。例如，使用UAG97.890版本的数据，我们可以将多个变量压缩到两个主成分中，从而在二维平面上观察数据的分布情况。这对于数据的分析、模型的评价和结果的解释具有重要意义。

2. 主成分分析法在各领域的应用

2.1 医疗健康

　　在医疗健康领域，PCA常用于患者数据的分析。比如，研究人员可以使用主成分分析法从大量的生理指标中提取出少数几个影响健康状况的关键因素。这不仅有助于提高疾病的早期诊断率，还能在疾病预防和健康管理上提供有效的指导。

2.2 市场营销

　　市场营销方面，PCA可以分析消费者行为数据，确定主要的购买动机和偏好。例如，一家企业可能会利用UAG97.890版本的消费者反馈数据，通过主成分分析识别出影响客户满意度的关键因素，从而更精准地制定市场策略和产品定位。

2.3 社会科学

　　在社会科学研究中，主成分分析法被广泛应用于问卷调查等数据的处理。研究者可以通过PCA识别出潜在的社会现象，帮助更深入的理解社会行为模式。

3. UAG97.890精选版的特点

　　2024年发布的UAG97.890精选版数据资料，在结构、清晰度和可用性上都有显著改善。这一版本对主成分分析的支持更加友好，使得用户在应用PCA技术时能够获得更佳体验。

3.1 数据的规范化

　　UAG97.890版数据进行了严格的预处理，确保每个变量都经过标准化处理，降低了用户在数据准备阶段的工作量。通过规范化的输入数据，模型的效果和稳定性得到了有效保证。

3.2 结果的可解释性

　　这个版本的数据分析结果更具可解释性。主成分分析法中提取的主成分不仅可以帮助用户识别数据的关键特征，同时也提供了每个主成分对应的具体含义，使得结果不再是单纯的数字，而是对实际问题的有力解释。

4. 案例分析：UAG97.890与主成分分析法的结合

　　在实际操作中，我们可以利用UAG97.890中的某一特定数据集作为实例，深入探讨主成分分析法如何提升数据分析的效率。例如，假设我们拥有一个包含1000名消费者购买行为的数据集，该数据集包括多个维度：年龄、性别、职业、购物频率、喜爱的产品类型等。

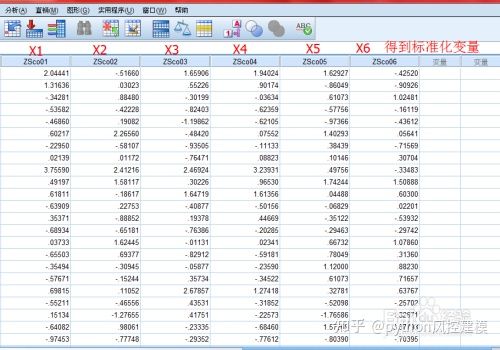
4.1 数据标准化过程

　　首先对数据进行标准化，以便后续的协方差计算。标准化后，我们得到了均值为0、方差为1的标准正态分布数据。

4.2 协方差矩阵计算

　　紧接着，利用标准化后的数据计算出协方差矩阵，这一过程帮助我们理解不同特征之间的关系。例如，购物频率与年龄之间的协方差能够帮助我们识别哪些年龄段的消费者更倾向于频繁购物。

4.3 主成分提取

　　在得到协方差矩阵后，进行特征值分解并提取主成分。假设我们提取到的前两个主成分分别解释了数据变异性的75%与15%，我们可以选择这两个主成分作为后续分析的基础。

4.4 可视化与决策支持

　　最终，我们将提取的主成分进行可视化，创建散点图与热力图，进而为市场策略的制定提供数据支持。这不仅使得分析结果更加直观，同时也为决策者提供了切实可行的依据。

5. 总结

　　主成分分析法作为一种有效的数据降维技术，有助于从复杂的数据集中提取有价值的信息。在2024新奥正版资料所提供的UAG97.890精选版中，我们看到了这一技术的应用前景与实践价值。通过实际案例的分析，我们更深入地认识到PCA在各行各业中的重要性，特别是在数据分析与决策支持方面。希望这一探索能激励更多的研究者与实践者将主成分分析法应用于实际问题解决中。